islat.blogg.se

1. #IN THE SIMPLE LINEAR REGRESSION EQUATION LET B HOW TO#
2. #IN THE SIMPLE LINEAR REGRESSION EQUATION LET B PLUS#

We have two more things we need to calculate.

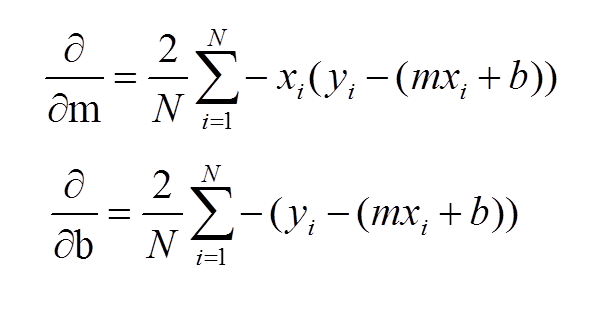
This means we’ve so far managed to find the values of 𝑛, the sum of 𝑥, and the sum of 𝑦. We get that the sum of 𝑦 is equal to 121.

#IN THE SIMPLE LINEAR REGRESSION EQUATION LET B PLUS#

So in this case the sum of 𝑦 is going to be 25 plus 18 plus 24 plus 25 plus 12 plus 17. We just want to add all of the values of 𝑦 in our table together. We see that it’s equal to 104.Īnd we can then do exactly the same thing to find the sum of 𝑦. So in this case, the sum of 𝑥 is 10 plus 22 plus 22 plus 13 plus 16 plus 21. We just need to add all of the 𝑥-values in our table together. We can also find the sum of 𝑥 and the sum of 𝑦 from our table. We can see that there are only six data points in this example. We can actually see this directly from our table. Once we’ve found these five values, we just need to substitute these into our formulae to find the values of 𝑎 and 𝑏. We need to find the value of 𝑛, the sum of 𝑥, the sum of 𝑦, the sum of 𝑥 times 𝑦, and the sum of 𝑥 squared. First, although this seems very complicated, there are only five things we need to find. However, there’s a lot of things we need to take in. We’re now ready to start finding the equation of our regression line. Similarly, the mean value of 𝑦 will be the sum of 𝑦 over 𝑛. The mean value of 𝑥 will be the total of all of our data points of 𝑥 divided by the number of data points.

#IN THE SIMPLE LINEAR REGRESSION EQUATION LET B HOW TO#

Similarly, we know how to find the average value of 𝑥 and 𝑦. We also need the formula for 𝑠 sub 𝑥𝑦, 𝑠 sub 𝑥𝑥, and 𝑦 bar and 𝑥 bar.įirst, we recall 𝑠 sub 𝑥𝑥 is equal to the sum of 𝑥 squared minus the sum of 𝑥 all squared over 𝑛 and 𝑠 sub 𝑥𝑦 is the sum of 𝑥 times 𝑦 minus the sum of 𝑥 times the sum of 𝑦 over 𝑛. Of course, this alone is not quite enough to find the values of 𝑎 and 𝑏. And our value of 𝑎 is going to be equal to 𝑦 bar minus 𝑏 times 𝑥 bar, where 𝑥 bar is the mean 𝑥-value and 𝑦 bar is the mean 𝑦-value. 𝑏 will be equal to 𝑠 sub 𝑥𝑦 divided by 𝑠 sub 𝑥𝑥, where 𝑠 sub 𝑥𝑦 is a measure between the covariance of 𝑥 and 𝑦 and 𝑠 sub 𝑥𝑥 is a measure of the variance of 𝑥. We recall to find the least squares regression line between two variables 𝑥 and 𝑦, we can use the following formula. To answer this question, let’s start by recalling how we find the least squares regression line linking two variables 𝑥 and 𝑦. We’re also told we only need to approximate the value of 𝑎 and 𝑏 to three decimal places. We’re told to give our answer in the form 𝑦 hat is equal to 𝑎 plus 𝑏𝑥. We need to use this table to find the equation of the regression line linking 𝑥 and 𝑦. In this question, we’re given a table of data points which show a relationship between two variables, the variable 𝑥 and the variable 𝑦. Approximate 𝑎 and 𝑏 to three decimal places. Find the equation of the regression line in the form 𝑦 hat is equal to 𝑎 plus 𝑏𝑥.

The table shows the relation between the variables 𝑥 and 𝑦.